Compte rendu des séances de l’Académie des Sciences
Séance du lundi 17 février 1851
[...
Mécanique - Suite de la note sur le mouvement du pendule simple en ayant égard à la révolution diurne de la Terre, par M. Binet
Première partie de la résolution
Les équations différentielles du mouvement relatif
d’un pendule simple d’une longueur r, en ayant égard à la rotation diurne de la
Terre résultent soit des formules de Laplace, établies dans le quatrième volume
de la Mécanique céleste, soit celle que Poisson a données dans le Journal
de l’École Polytechnique, 26e cahier, je vais rapporter ces formules en me
servant, à peu près de la notation de Poisson : n sera la vitesse
angulaire de la Terre de l’occident vers l’orient, γ la latitude
géographique du point de suspension du pendule ; g la pesanteur terrestre
combinée avec la force centrifuge locale provenant de la rotation de la
Terre ; les coordonnées rectangulaires x, y, z auront leur origine au
point de suspension ; l’axe positif des x est dirigé vers l’Est, l’axe de
y vers le Nord, et les z positifs sont dirigés de haut en bas, dans le sens
vertical de la chute des graves ; N est la tension du fil du pendule
simple, ou la pression normale que supporte la surface sphérique : cette
force est dirigée vers l’origine des coordonnées, et elle forme avec les axes
des angles qui ont ![]() ,
, ![]() ,
, ![]() pour cosinus. En
négligeant la résistance de l’air, les trois équations différentielles du
mouvement du pendule seront :
pour cosinus. En
négligeant la résistance de l’air, les trois équations différentielles du
mouvement du pendule seront :
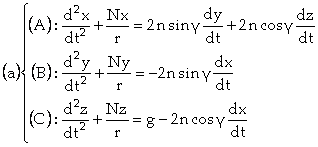
Entre les coordonnées, on a ![]() d’où l’on tire les
relations
d’où l’on tire les
relations ![]() et
et ![]() .
.
En multipliant par dx, dy, dz les équations
(a) et en les ajoutant, tous les termes affectés de N et de n se détruisent, et
il reste simplement ![]() dont l’intégrale est
dont l’intégrale est ![]() .
.
On aura la pression N en multipliant par x, y,
z les mêmes équations différentielles et en les ajoutant ; on remplacera
dans la somme ![]() par
par ![]() , et il viendra
, et il viendra
![]() .
.
On substitue la valeur ![]() , au carré de la vitesse, et il vient
, au carré de la vitesse, et il vient
![]() .
.
La vitesse angulaire de la Terre, représentée
par le coefficient n dans ces formules, est une très petite fraction, savoir ![]() , si l’on prend la seconde sidérale comme unité de temps, et
alors,
, si l’on prend la seconde sidérale comme unité de temps, et
alors, ![]() de degré ; et
quand on prend la seconde de temps moyen solaire
de degré ; et
quand on prend la seconde de temps moyen solaire ![]() , ce qui surpasse un peu la première valeur, rapportée à une
autre unité de temps.
, ce qui surpasse un peu la première valeur, rapportée à une
autre unité de temps.
Tous les termes multipliés par n peuvent être assimilés à des forces perturbatrices du mouvement déterminé par les mêmes équations où l’on aurait posé n=0 : ce seraient alors les équations du pendule conique dont on a les intégrales qui renferment quatre paramètres arbitraires ; pour avoir égard aux termes multipliés par n, selon la méthode connue de la variation des constantes arbitraires, on rendra variables les quatre paramètres ; et leurs différentielle étant obtenues pourront être intégrées par approximation.
Notre objet actuel permet de simplifier cette
recherche, parce que nous pouvons nous borner à considérer les petites
digressions ou oscillations d’un pendule autour de sa position d’équilibre,
autour de la verticale, sa distance ![]() à l’axe des z doit
demeurer une petite quantité, ainsi que les vitesses
à l’axe des z doit
demeurer une petite quantité, ainsi que les vitesses ![]() ,
, ![]() ,
, ![]() , elles seront traitées comme des quantités du premier ordre.
, elles seront traitées comme des quantités du premier ordre.
On a ![]() ainsi, en voulant
négliger les
ainsi, en voulant
négliger les ![]() dans z, on aura
dans z, on aura ![]() . En remplaçant z par cette valeur dans la dernière des
formules de (a), on aura
. En remplaçant z par cette valeur dans la dernière des
formules de (a), on aura 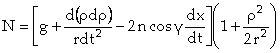 où
où ![]() remplace le facteur
remplace le facteur ![]() : dans la première approximation, on peut négliger le
terme
: dans la première approximation, on peut négliger le
terme ![]() , ainsi que les termes en
, ainsi que les termes en ![]() et
et ![]() qui demeurent du
second ordre : on y aura égard si on le veut dans une approximation
ultérieure. La valeur de N sera ainsi réduite à
qui demeurent du
second ordre : on y aura égard si on le veut dans une approximation
ultérieure. La valeur de N sera ainsi réduite à ![]() .
.
Pour abréger, nous poserons ![]() , et les deux premières équations (a) deviendront :
, et les deux premières équations (a) deviendront :
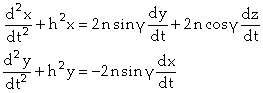
Le terme ![]() doit être rejeté dans
l’approximation suivante, étant de l’ordre déjà négligé dans le premier membre
où N est remplacé par
doit être rejeté dans
l’approximation suivante, étant de l’ordre déjà négligé dans le premier membre
où N est remplacé par ![]() . Les équations deviennent donc en posant
. Les équations deviennent donc en posant ![]() ,
,
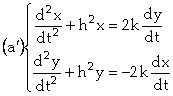
On satisfait à ces équations linéaires par les
valeurs ![]() et
et ![]() , p et
, p et ![]() étant deux constantes
arbitraires, et
étant deux constantes
arbitraires, et ![]() une quantité constante
qui va être déterminée. La substitution dans l’une ou l’autre des équations (a)
donne la même formule, savoir
une quantité constante
qui va être déterminée. La substitution dans l’une ou l’autre des équations (a)
donne la même formule, savoir ![]() . Après avoir divisé par
. Après avoir divisé par ![]() , cela se réduit à
, cela se réduit à ![]() . On obtiendra
. On obtiendra ![]() en résolvant
l’équation
en résolvant
l’équation ![]() , ses racines
, ses racines ![]() et
et ![]() sont de signes
contraires, savoir,
sont de signes
contraires, savoir, ![]() et
et ![]() . On remarquera que
. On remarquera que ![]() est une quantité
négligeable relativement à
est une quantité
négligeable relativement à ![]() , parce que
, parce que ![]() et nous prendrons
et nous prendrons ![]() et
et ![]() . On satisfait évidemment aux mêmes équations (a’) par les
valeurs
. On satisfait évidemment aux mêmes équations (a’) par les
valeurs ![]() et
et ![]() ; or les équations différentielles étant linéaires,
l’on sait que les expressions générales des variables x et y se composent de la
somme des valeurs particulières, ainsi, l’on a
; or les équations différentielles étant linéaires,
l’on sait que les expressions générales des variables x et y se composent de la
somme des valeurs particulières, ainsi, l’on a ![]() et
et ![]() .
.
L’instant à partir duquel on compte le temps
étant arbitraire, on pourra rendre égales les constantes arbitraires ![]() ; la constante ainsi supprimée sera comprise dans la
variable t : les deux autres constantes p et p1, quoique
arbitraires, doivent cependant être telles que x et y demeurent de petites
quantités, selon l’hypothèse. Ajoutons les carrés des coordonnées
; la constante ainsi supprimée sera comprise dans la
variable t : les deux autres constantes p et p1, quoique
arbitraires, doivent cependant être telles que x et y demeurent de petites
quantités, selon l’hypothèse. Ajoutons les carrés des coordonnées ![]() cela donne, pour
cela donne, pour ![]() ,
, ![]() parce que
parce que ![]() .
.
Cette valeur revient à ![]() et en posant
et en posant ![]() et
et ![]() , on aura
, on aura![]() . Ainsi la valeur de
. Ainsi la valeur de ![]() est nécessairement
comprise entre
est nécessairement
comprise entre ![]() et
et ![]() , et, en posant que
, et, en posant que ![]() soit supérieur à
soit supérieur à ![]() , on aura constamment
, on aura constamment ![]() . Par conséquent, il suffit que la constante
. Par conséquent, il suffit que la constante ![]() soit une petite
quantité pour que ces résultats soient conformes à l’hypothèse des petites
oscillations.
soit une petite
quantité pour que ces résultats soient conformes à l’hypothèse des petites
oscillations.
Seconde partie de la résolution
On voit qu’après chaque durée ![]() la distance
la distance ![]() reprend périodiquement
sa valeur, mais il n’en n’est pas tout à fait ainsi de x et y : ces
coordonnées éprouvent de petites altérations dont nous allons reconnaître les
effets. Substituons dans x et y pour
reprend périodiquement
sa valeur, mais il n’en n’est pas tout à fait ainsi de x et y : ces
coordonnées éprouvent de petites altérations dont nous allons reconnaître les
effets. Substituons dans x et y pour ![]() et
et ![]() les quantités
les quantités ![]() et
et ![]() ; elles deviennent
; elles deviennent ![]()
ou bien 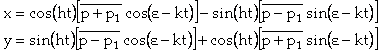 or
or ![]() et
et ![]() , on a donc
, on a donc ![]() , d’où l’on tire
, d’où l’on tire
![]()
Pour interpréter plus clairement ces expressions, nous concevrons le pendule simple (ou l’extrémité du rayon sphérique) comme projeté sur le plan tangent horizontal, inférieur à la sphère décrite avec le rayon r ; nous nommerons P cette projection mobile à l’égard de deux axes des x et y parallèles à ceux qui passaient par le point de suspension ; le point mobile ne s’écartant du plan tangent inférieur que d’une quantité du second ordre, est dans toutes ces situations extrêmement voisin de sa nouvelle projection : suivre des yeux cette projection est presque suivre des yeux le pendule lui-même.
Soit ![]() l’azimut de la
projection horizontale P mesurée de l’Est vers le Nord, c’est-à-dire dans le
sens de circulation des x positifs aux y positifs ; en sorte que
l’azimut de la
projection horizontale P mesurée de l’Est vers le Nord, c’est-à-dire dans le
sens de circulation des x positifs aux y positifs ; en sorte que ![]() et
et ![]() ; par les valeurs précédentes, on aura
; par les valeurs précédentes, on aura ![]() ou bien
ou bien ![]() et semblablement
et semblablement ![]() .
.
Soit encore ![]() et
et ![]() ;
on voit que ξ est la projection du point P sur une droite qui comprendra
;
on voit que ξ est la projection du point P sur une droite qui comprendra ![]() avec l’axe des x, car
elle forme alors l’angle
avec l’axe des x, car
elle forme alors l’angle ![]() avec ρ ;
ν sera la perpendiculaire abaissée de P sur cette même droite ; et
ξ est donc une droite mobile. Cela posé, on a
avec ρ ;
ν sera la perpendiculaire abaissée de P sur cette même droite ; et
ξ est donc une droite mobile. Cela posé, on a ![]() et
et ![]() et en ajoutant les carrés de ces valeurs,
et en ajoutant les carrés de ces valeurs, ![]() ainsi les coordonnées
ν et ξ appartiennent à une ellipse dont les axes
ainsi les coordonnées
ν et ξ appartiennent à une ellipse dont les axes ![]() et
et ![]() sont constants ;
mais le grand axe de cette ellipse est uniformément mobile autour de son
centre. La valeur de l’angle azimutal
sont constants ;
mais le grand axe de cette ellipse est uniformément mobile autour de son
centre. La valeur de l’angle azimutal ![]() prouve que le sens du
mouvement est rétrograde du nord vers l’est, la vitesse angulaire constante
prouve que le sens du
mouvement est rétrograde du nord vers l’est, la vitesse angulaire constante ![]() , étant
, étant ![]() , où γ est la latitude. Cette vitesse est nulle quand la
station est à l'équateur où
, où γ est la latitude. Cette vitesse est nulle quand la
station est à l'équateur où ![]() ; elle serait
; elle serait ![]() pour une station
polaire. Quand on pose
pour une station
polaire. Quand on pose ![]() , selon l'hypothèse ordinaire où l'on néglige la rotation de la
terre, la projection devient l'ellipse invariable indiquée par M. Pouillet,
dans le cas de des petites oscillations du pendule simple.
, selon l'hypothèse ordinaire où l'on néglige la rotation de la
terre, la projection devient l'ellipse invariable indiquée par M. Pouillet,
dans le cas de des petites oscillations du pendule simple.
La durée d’une oscillation étant![]() , la déviation de l’axe de l’ellipse est, pendant ce temps,
de
, la déviation de l’axe de l’ellipse est, pendant ce temps,
de ![]() ;
quantité extrêmement petite, mais qui, se reproduisant dans le même sens à
chaque oscillation, devient promptement sensible et appréciable.
;
quantité extrêmement petite, mais qui, se reproduisant dans le même sens à
chaque oscillation, devient promptement sensible et appréciable.
La vitesse angulaire du plan oscillatoire
autour de la verticale est ![]() ; il convient de remarquer qu'elle est précisément
égale en grandeur, et de direction contraire à une composante de la vitesse de rotation
de la terre n décomposée en deux vitesses angulaires : l'une aurait, pour axe
de rotation la verticale, et l'autre, la méridienne dirigée vers le nord. Ces
deux droites et une parallèle à l’axe de la terre passant par le point de
suspension du pendule sont dans un même plan ; la parallèle à l’axe de la
terre fait avec la méridienne, l’angle γ, et l’angle
; il convient de remarquer qu'elle est précisément
égale en grandeur, et de direction contraire à une composante de la vitesse de rotation
de la terre n décomposée en deux vitesses angulaires : l'une aurait, pour axe
de rotation la verticale, et l'autre, la méridienne dirigée vers le nord. Ces
deux droites et une parallèle à l’axe de la terre passant par le point de
suspension du pendule sont dans un même plan ; la parallèle à l’axe de la
terre fait avec la méridienne, l’angle γ, et l’angle ![]() avec la
verticale ; d’après le théorème d’Euler sur les vitesses angulaires de
rotation, la composante de n avec la verticale est
avec la
verticale ; d’après le théorème d’Euler sur les vitesses angulaires de
rotation, la composante de n avec la verticale est ![]() . Ainsi l’angle azimutal s’accroît comme si la terre était
entraînée autour de la verticale par la composante horizontale de sa vitesse
angulaire, et que le plan oscillatoire fût entièrement fixe, sans avoir égard à
la seconde composante
. Ainsi l’angle azimutal s’accroît comme si la terre était
entraînée autour de la verticale par la composante horizontale de sa vitesse
angulaire, et que le plan oscillatoire fût entièrement fixe, sans avoir égard à
la seconde composante ![]() . Au pôle, cette dernière composante est nulle ; la
proposition est alors évidente et c’est le point de départ des considérations
ingénieuses qui ont amené M. Foucault à son expérience.[...]
. Au pôle, cette dernière composante est nulle ; la
proposition est alors évidente et c’est le point de départ des considérations
ingénieuses qui ont amené M. Foucault à son expérience.[...]
Résolution de l’équation du pendule à la manière de Binet
Première partie de la résolution
Pour la résolution de l’équation différentielle des mouvements du pendule de Foucault, telle que Jacques Binet l’a menée, on part du système d’équations que Poisson a établi par différents changements de base, à savoir :
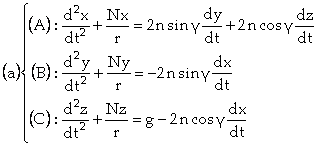
Remarque : N,
que Jacques Binet nomme « pression », n’est pas une tension en
réalité. Calculons l’unité de N : ![]() . Donc N s’exprime en
. Donc N s’exprime en ![]() . On pouvait également le remarquer en notant que les
équations ont été obtenues grâce à la relation fondamentale de la dynamique
puis en divisant les équations obtenues par la masse de la sphère suspendue au
fil.
. On pouvait également le remarquer en notant que les
équations ont été obtenues grâce à la relation fondamentale de la dynamique
puis en divisant les équations obtenues par la masse de la sphère suspendue au
fil.
Le fil reliant la sphère à son point d’attache
étant inextensible, on a ![]() . Donc, en différentiant cette équation une fois, puis deux
fois, on obtient les équations suivantes :
. Donc, en différentiant cette équation une fois, puis deux
fois, on obtient les équations suivantes :
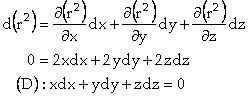 et
et 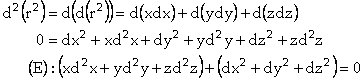
On obtient une nouvelle équation à partir des relations entre les différentielles et du système d’équations du pendule de Foucault :

On intègre cette équation :

Dans (G), c est une constante d’intégration.
Remarque : On
peut retrouver cette équation à partir du théorème de l’énergie
cinétique ; en effet, on a, d’une part, la puissance du poids qui vaut ![]() d’où
d’où ![]() où m est la masse de
la sphère suspendue au fil, et d’autre part,
où m est la masse de
la sphère suspendue au fil, et d’autre part, 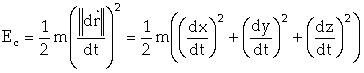 , et puisque l’on a égalité entre les deux, on retrouve le
résultat.
, et puisque l’on a égalité entre les deux, on retrouve le
résultat.
En substituant les valeurs ainsi déterminées dans (a), il vient :

Or ![]() est négligeable devant
les autres termes et :
est négligeable devant
les autres termes et : 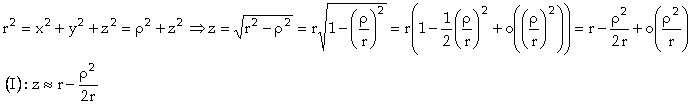
(On effectue un DL1(0) de ![]() , possible car x et y sont négligeables devant z, donc
, possible car x et y sont négligeables devant z, donc ![]() est négligeable devant
r :
est négligeable devant
r : ![]() ).
).
À partir de là, on dérive z par rapport au
temps, et il vient :
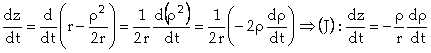
D’où, en réalisant un DL1(0) de ![]() à partir de l’équation
(C) :
à partir de l’équation
(C) :

Lorsqu’on néglige les termes du second ordre,
c’est-à-dire, ![]() ,
, ![]() et le terme
et le terme ![]() (négligeable car n est
petit de même que
(négligeable car n est
petit de même que ![]() , on peut le considérer comme un terme du second ordre). On a
, on peut le considérer comme un terme du second ordre). On a
![]() .
.
Remarque : Ce
résultat est prévisible étant donné que les oscillations sont de faible
amplitude, donc la tension du fil est quasiment verticale puisqu’elle suit sa
direction. De plus, à l’équilibre, le poids et la tension du fil s’annulent,
d’après la relation fondamentale de la dynamique.
On note maintenant ![]() , mais aussi
, mais aussi ![]() . On obtient alors, en remplaçant N et
. On obtient alors, en remplaçant N et ![]() par leurs valeurs dans
(a) :
par leurs valeurs dans
(a) :
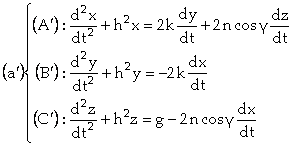 .
.
Or ![]() qui est assimilable à
un terme du second ordre, puisqu’il comporte n, vitesse angulaire de rotation
de la Terre, qui est petite et
qui est assimilable à
un terme du second ordre, puisqu’il comporte n, vitesse angulaire de rotation
de la Terre, qui est petite et ![]() qui est une quantité
du premier ordre. On peut donc négliger ce terme. On trouve donc :
qui est une quantité
du premier ordre. On peut donc négliger ce terme. On trouve donc :
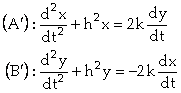 .
.
Selon Jacques Binet, les solutions sont de la
forme ![]() .
.
Remarque : Ces
solutions ne sont pas justifiées. En effet, à l’époque de la publication de cet
ouvrage, lorsqu’une solution était juste, on considérait que toutes les
solutions étaient de cette forme (si une solution convenait, alors, les autres
étaient de la même forme). Aujourd’hui, on retrouve ces résultats grâce à la
méthode complexe. En effet, ![]() . Si on considère le complexe
. Si on considère le complexe ![]() , on obtient l’équation différentielle linéaire d’ordre deux
, on obtient l’équation différentielle linéaire d’ordre deux ![]() . Alors, on retrouve les mêmes solutions que Binet : l’équation
caractéristique associée à l’équation différentielle ci-dessus est
. Alors, on retrouve les mêmes solutions que Binet : l’équation
caractéristique associée à l’équation différentielle ci-dessus est ![]() et a pour solutions r
et r1 tels que
et a pour solutions r
et r1 tels que 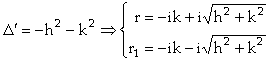 , donc les solutions pour u sont
, donc les solutions pour u sont ![]() , on peut en conclure que les solutions pour x et y sont de
la forme :
, on peut en conclure que les solutions pour x et y sont de
la forme :
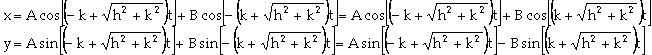 On a donc ici les valeurs de μ, μ1,
ε et ε1.
On a donc ici les valeurs de μ, μ1,
ε et ε1.
On a alors
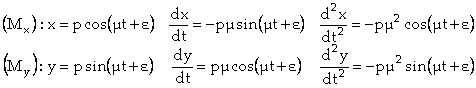 . Si on reporte ces valeurs dans
. Si on reporte ces valeurs dans ![]() , on obtient l’équation du second degré en
, on obtient l’équation du second degré en ![]() :
:
![]() . De même, le report de ces mêmes valeurs dans l’équation
. De même, le report de ces mêmes valeurs dans l’équation ![]() permet de retrouver le
résultat précédent :
permet de retrouver le
résultat précédent :
![]() On peut maintenant résoudre cette équation
On peut maintenant résoudre cette équation ![]() donc, les solutions
sont
donc, les solutions
sont ![]() et
et ![]() .
.
Or ![]() et
et ![]() , donc
, donc ![]() est négligeable devant
est négligeable devant
![]() , on peut donc considérer que
, on peut donc considérer que ![]() et
et ![]() .
.
Les solutions de l’équation différentielle
sont de la forme ![]() et
et ![]() .
.
Binet pose ensuite ![]() .
.
Remarque : On a vu, dans la résolution moderne de l’équation du pendule, que la résolution de l’équation différentielle donnant le complexe u en fonction du temps donne l’égalité entre ε, ε1 et zéro.
 En
remplaçant par leurs valeurs les quantités μ et μ1, on
obtient :
En
remplaçant par leurs valeurs les quantités μ et μ1, on
obtient :
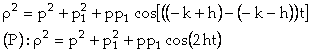 , que
l’on transforme :
, que
l’on transforme :
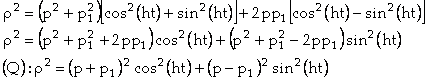
On pose deux nouvelles inconnues : ![]() et
et ![]() . On a donc
. On a donc ![]() . Étudions la fonction
. Étudions la fonction ![]() en fonction du
temps :
en fonction du
temps :
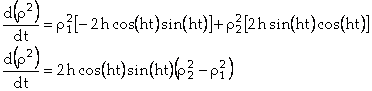 . si on suppose
. si on suppose ![]() , on a le tableau de variation suivant :
, on a le tableau de variation suivant :
|
t |
0 |
|
|
|
|
|||||||||||
|
|
+ |
- |
- |
+ |
||||||||||||
|
|
+ |
+ |
- |
- |
||||||||||||
|
|
- |
- |
- |
- |
||||||||||||
|
|
- |
+ |
- |
+ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Les variations de ![]() nous indiquent
clairement que
nous indiquent
clairement que ![]() :
:
Donc, il est nécessaire que ![]() soit une petite quantité
pour que ρ soit une petite quantité, c’est-à-dire, pour que l’on se trouve
dans le cadre de petites oscillations. Et par définition,
soit une petite quantité
pour que ρ soit une petite quantité, c’est-à-dire, pour que l’on se trouve
dans le cadre de petites oscillations. Et par définition, ![]() , où p et p1 sont des réels tels que
, où p et p1 sont des réels tels que ![]() et
et ![]() . Les longueurs x et y restant négligeables devant r ; p
et p1 restent eux aussi négligeable devant r, donc,
. Les longueurs x et y restant négligeables devant r ; p
et p1 restent eux aussi négligeable devant r, donc, ![]() est une petite
quantité.
est une petite
quantité.
Seconde partie de la résolution
ρ est périodique, c’est-à-dire qu’on
remarque qu’après chaque période ![]() , ρ reprend la même valeur (
, ρ reprend la même valeur (![]() ). Mais il n’en va pas de même pour x et y :
). Mais il n’en va pas de même pour x et y :
Remplaçons μ et μ1 par
leurs valeurs (respectivement ![]() et
et ![]() ) dans l’expression de x et de y :
) dans l’expression de x et de y :

que l’on transforme de sorte que cela
devienne :
 On
remplace
On
remplace ![]() et
et ![]() par leur valeur
respective
par leur valeur
respective ![]() et
et ![]() , on a donc
, on a donc 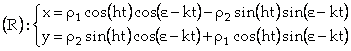 . D’où l’on tire l’expression de
. D’où l’on tire l’expression de ![]() et de
et de ![]() en fonction de x, y,
en fonction de x, y, ![]() et
et ![]() :
:



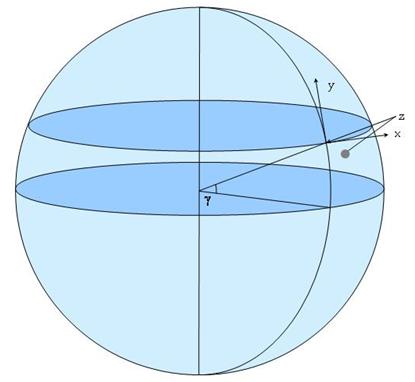
On considère maintenant que les coordonnées x
et y de la sphère suspendue au fil sont celles du projeté P de la sphère sur le
sol comme décrit par le schéma suivant :
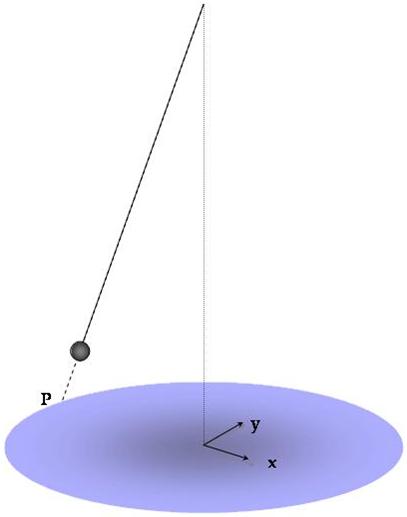
Ceci est possible étant donné qu’on se trouve
dans le cas de petites oscillations, donc la sphère rase le sol et se trouve
non loin de P.
Soit ![]() tel que
tel que ![]() et
et ![]()
Remarque : Binet
appelle υ un « azimut de la projection horizontale P mesurée de l’Est
vers le Nord », c’est-à-dire une direction ; mais, en réalité,
puisque ![]() et
et ![]() ,
on peut considérer que l’on se place en coordonnées polaires où ρ et
υ sont les coordonnées polaires, ρ étant la distance de P au pôle et
υ l’angle entre l’axe polaire des x et la droite (OP).
,
on peut considérer que l’on se place en coordonnées polaires où ρ et
υ sont les coordonnées polaires, ρ étant la distance de P au pôle et
υ l’angle entre l’axe polaire des x et la droite (OP).
En remplaçant les coordonnées cartésiennes x
et y par les coordonnées polaires de P ρ et υ dans les équations (S),
on obtient :

À partir de maintenant, on notera ![]() et
et ![]() . Concrètement, on remarque que, puisque
. Concrètement, on remarque que, puisque ![]() et
et ![]() et
et ![]() ,
ξ et ν sont les projections de P dans un plan tel que les coordonnées
polaires de P soient ρ et ν, on a donc un axe polaire en décalage par
rapport à l’axe des x, et ce décalage vaut
,
ξ et ν sont les projections de P dans un plan tel que les coordonnées
polaires de P soient ρ et ν, on a donc un axe polaire en décalage par
rapport à l’axe des x, et ce décalage vaut ![]() :
on note ξ l’axe des abscisses et ν celui des coordonnées dans cette
nouvelle base, qui, il faut le rappeler, est mobile dans le repère (Oxyz), en
effet, l’angle
:
on note ξ l’axe des abscisses et ν celui des coordonnées dans cette
nouvelle base, qui, il faut le rappeler, est mobile dans le repère (Oxyz), en
effet, l’angle ![]() où S est la projection
orthogonale au sol du point de suspension du pendule, vaut
où S est la projection
orthogonale au sol du point de suspension du pendule, vaut ![]() et dépend donc du
temps.
et dépend donc du
temps.
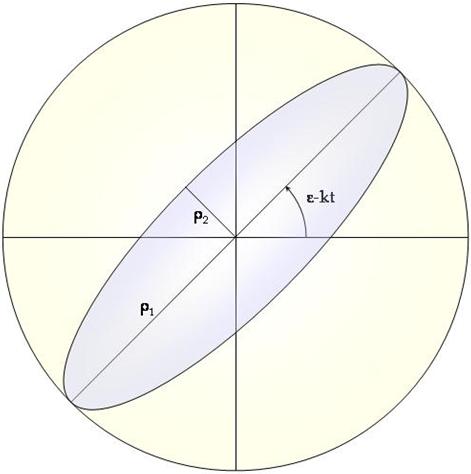
On a donc ![]() et
et ![]() . Ces relations donnent l’équation :
. Ces relations donnent l’équation :  .
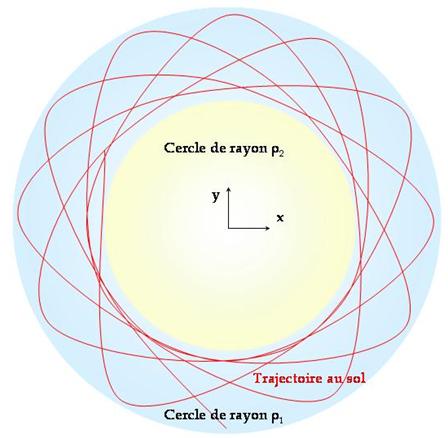
.
Ceci est l‘équation d’une ellipse, en effet,
ρ1 et ρ2 sont fixés, donc, ξ et ν
sont les coordonnées d’un point qui décrit une ellipse, donc le grand axe est ![]() et le petit axe est
et le petit axe est ![]() . Mais il ne faut pas oublier que le grand axe de cette
ellipse possède un mouvement rétrograde par rapport à la rotation de la Terre,
tel que l’orientation de cet axe par rapport à l’axe de référence des x soit de
. Mais il ne faut pas oublier que le grand axe de cette
ellipse possède un mouvement rétrograde par rapport à la rotation de la Terre,
tel que l’orientation de cet axe par rapport à l’axe de référence des x soit de
![]() .
.
Interprétation des résultats obtenus
Lorsqu’on donne un mouvement au pendule,
l’oscillation se trouve dans le plan ![]() . La vitesse de rotation du plan du pendule est donc de
. La vitesse de rotation du plan du pendule est donc de ![]() , soit, en valeur absolue,
, soit, en valeur absolue, ![]() .
.
Si on se trouve au pôle, on a ![]() , donc
, donc ![]() , le plan d’oscillation du pendule tourne à la même vitesse
que la Terre ; au contraire, si on se trouve à l’équateur,
, le plan d’oscillation du pendule tourne à la même vitesse
que la Terre ; au contraire, si on se trouve à l’équateur, ![]() , donc
, donc ![]() , c’est-à-dire que le plan d’oscillation du pendule ne change
pas, on se trouve dans le cas du pendule simple dans un référentiel galiléen, comme
si on négligeait la rotation de la Terre.
, c’est-à-dire que le plan d’oscillation du pendule ne change
pas, on se trouve dans le cas du pendule simple dans un référentiel galiléen, comme
si on négligeait la rotation de la Terre.
|
Durée d’une oscillation |
|
|
Déviation du plan du pendule pendant une oscillation |
|
|
Vitesse de rotation du plan d’oscillation du pendule |
|
Jean Léon Foucault fût un véritable touche à tout génial. Rares sont les disciplines scientifiques où il ne laissa pas sa trace. D’un point de vue pratique, nous sommes aujourd’hui les héritiers de son gyroscope, de sa méthode dite de « Foucaultage » (contrôle de la surface des miroirs encore utilisé par les astronomes et les opticiens) mais aussi dans le domaine de la microphotographie ou des télescopes. D’un point de vue théorique, il apporta également une contribution non négligeable que ce soit par ses mesures de la vitesse de la lumière ou par ses recherches sur les courants dits de « Foucault ».
C’est par cet équilibre entre recherches fondamentales et recherches appliquées que vient l’originalité du savant qu’était Foucault et qui ont fait de lui le grand chercheur que nous connaissons.
Toutefois c’est surtout pour l’expérience du pendule qui porte son nom que l’on se souvient de Foucault. En effet, cette dernière s’est distinguée des autres expériences scientifiques qui sont le plus souvent réservées aux initiés, par la relative simplicité de sa mise en œuvre et le fait qu’elle mettait à la portée du regard de tous, du plus grand physicien au plus modeste citoyen, la rotation de la Terre. Son caractère spectaculaire fit sa grande popularité qui provoqua une véritable manie du pendule à travers le monde. Dans le cercle restreint des physiciens, cette expérience fut le prétexte à de nombreuses théories plus ou moins proches de la réalité qui, d’un côté, révélèrent des erreurs commises par certains par le passé et de l’autre, confirmèrent des travaux alors non vérifié par la pratique.
Dans la continuité de cette expérience, Foucault créa le gyroscope, outil qui a eu et qui a encore une importance capitale de nos jours, avec les gyro-lasers, dans le domaine de l’aéronautique ou de la marine.
Aujourd’hui, Foucault n’est pas oublié, son pendule est devenu, en quelque sorte, une œuvre d’art que l’on peut admirer partout dans le monde que ce soit en Europe, aux Amériques, en Asie ou sur tout autre continent et qui continue à fleurir ici et là.