Also available : french version

Introduction

Subject
The growth of plants or the development of embryos needs complex phenomenons wich lead to a high organisation of constituted atoms and molecules. The biology gives a great deals of examples for this collective behaviour. Some chemical systems with a limited number of reactants, can spontanously organise themselves. We class these phenomenons in two categories :

• in a homogenous system, we can observe a self organisation in the time (like in oscillating reactions) ;
• the couplage between diffusion and chemical reaction can creat self spatial organisation.

Spatial patterns

What is an oscillating reaction ?
A macroscopic reaction can be explained by a mechanism consisting of a great deal of elementary reactions in the microscopic scale. In these reactions, or steps, some species are created and then consumed. In most chemical reactions, the concentrations of species depend monotonously on the time but in an oscillating reaction, the concentrations of some species increase and then decrease during the time, between two limits. Some properties like colour, absorption or average potential can change during the experiment with a more or less periodical evolution. Due to these facts, some of these oscillating reactions are used as chemical clocks.

Some historical dates

• The Bray-Liebhafsky reaction
  In 2001, there was the eightieth anniversary of the first oscillating reaction by W. C. Bray of the university of California at Berkeley. This reaction was the decomposition of H₂O₂ in O₂ and H₂O with IO₃^-. The study of this reaction was made by Bray and one of his students Hermann Liebhafsky. In 1973 two teachers, Briggs et Rausher added CH₂(CO₂H)₂ and Mn²⁺ ; the oscillations were accentuated and their periods reduced to a few seconds. We can summarize the phenomenon by the following equations :
  
  
  
  
  
  
• The Belousov-Zhabotinsky reaction
  The most known oscillating reaction is the one discovered by the Russian biochemist Boris Pavlovich Belousov in 1950. Belousov was interested in the Krebs cycle and the importance of the citric acid. The dosing entity was BrO₃^- in an acidic solution and Ce⁴⁺ was the catalytic compound. During the reaction, the citric acid was oxidised in CO₂ and BrO₃^- reduced in Br^-. Belousov used a redox indicator to see the end of the reaction. Instead of observing a change of colour at the end of the reaction, he noticed that a periodic colour appeared reguraly during the evolution. Belousov tried to study the phenomenon and wanted to publish his work in 1951 but his publication was refused because his results seemed to be contrary to the laws of thermodynamics.
  In 1961, Anatol Zhabotinsky, a student in biophysic at the University of Moscow, worked on this reaction. He replaced the citric acid by malonic acid and observed oscillations with larger amplitudes [34]. The reaction was :
  
  
  This results didn't interest the occidental europ or the US because of the political context in this period. During years, the Belousov-Zhabotinsky reaction remained a laboratory curiosity [6].

Experimental aspect
The following reaction is the Belousov-Zhabotinsky reaction. It isn't difficult. We begin to prepare 5 aqueous solutions with concentration in units of mol.L^-1. Then, we mix these solutions in a big beaker, increase the temperature around 25 °C and stir well. The oscillations appear after some seconds [11], [12].

• The variation of potential leads to a modification in the colour of the indicator : the ferroin, which is a complex between Fe (II) and the 1, 10-phenantrolin (ophen).

  

  The oxydized form is blue and the reduced one is red. The colour changes when the average potential reaches the value of : E⁰ = 1, 1 V

The opposite animation gives an approximative idea of the phenomenon observed during the Belousov-Zhabotinsky reaction. The colour changes from red to blue. Whithout indicator, the colour changes from yellow to colourless. The manipulation must be done under an efficient hood. Br2 appearing at the end of the reaction.

• The evolution of potential can be followed with an electrochemical method : the working electrode is in platinium, and the referencing one is constituted with saturated Hg₂SO₄.

  

  The electrodes are linked at the analogic entering of a PC-MES 2 card (Eurosmart) and the results are treated by SYNCHRONIE program.

The graph, giving the average potential (pot) during the time is representated below :

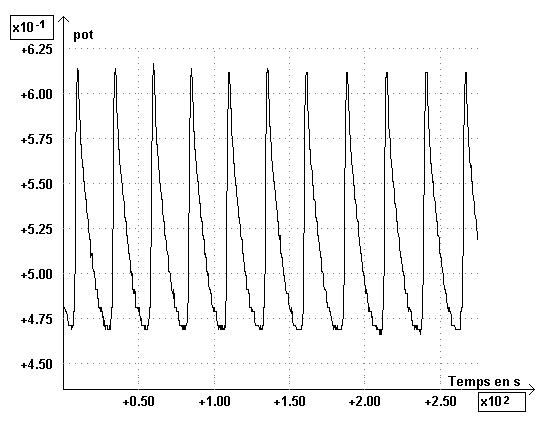
The Fourier analysis of the graph can be obtained by SYNCHRONIE program, and we observe one fundamental frequency, showing the periodicity of the phenomenon. The presence of harmonics is due to the non sinusoïdal nature of signal. We have realized a chemical clock.

• As we'll see after, a necessary condition for the observation of oscillations is that the chemical system evoluates far from the thermodynamic equilibrium. When the reaction is done in a closed reactor, we can only see the phenomenon during a short time ; this is a transitional system dealing near the equilibrium. For this reason an opened reactor is used in research experiments, feeded continously with reactants while the products are continously extracted after their formation. We'll find the description of this reaction in the CRPP site [19]. It's interested to follow the evolution with a characteristic of the system. In the case of the BZ reaction, we follow the evolution with spectrometric absorption method at the wavelenght of l = 340 nm where Ce⁴⁺ are the sole ions to absorb. We can also follow the evolution of Br^- concentration with a specific electrode for Br^-, this last method was used by R. M. Noyes, R. J. Fields and E. Korös in their research of the reaction mechanism.

The BZ reaction mechanism
The complete mechanism of the BZ reaction was made by R. M. Noyes, R. J. Fields and E. Körös. It counts 18 réactions with 21 différent chemical species. A simplified mechanism was proposed by the same authors. It was named "Oregonator" in reference to the University of Oregon where they worked in this period. The different steps of this mechanism are done below :

Kinetic models
A lot of kinetic models were proposed to describe the BZ reaction. To simplify the equations we'll use the following notations :

Compound	BrO3-	Orga	HBrO	HBrO2	Br-	Ce4+
Notation	A	B	P	X	Y	Z

Then, the simplified mechanism of FKN, limited to the steps (a), (d'), (e), (f) and (h) is :

[B] represents all the organic compounds and in this simplified mechanism, its concentration is supposed constant. f is and adjusted parameter which can evoluate from 0,5 to 2,4. Each step (i) is characterized by a kinetic constant k_i and then :

This system isn't linear. Some results can be obtained by numerical methods. We observe oscillating results for f values from 0,5 to 2,4.

Chaotic system
The seventies developped some important works about non linear phenomenons. One of the most great conclusion of these studies is that some dynamic systems belonging to various parts of physic have unexpected behaviour although they are described by determinist rules. These systems have a large sensitivity to the initial conditions, and are named "determinist chaos". It's logical to wonder if the BZ reaction, which dynamic behaviour is described by non linear equations, can have a chaotic behaviour. Some experiments, done by Schmitz and Hudson in 1977, showed the appearance of chaos in the BZ reaction. And then, the BZ reaction permitted to test some theoretical aspects of dynamic systems [5], [24].

Self-spatial organization

Diffusion phenomenon
Put gently a drop of ink in a beaker full of water. The ink ends up invading all the solution. When a solution is quiet with a uniform temperature, the convection phenomenon can be neglected. In these conditions, it's the diffusion which provides the transport of compounds. A spontaneous transfer appears from the zones of high concentrations to these ones of lower concentrations. With self-catalytic reactions like BZ reaction, the situation is completly different. The coupling between chemical reaction and diffusion can create organizations in space. We can observe two phenomenons of organization :

• one implies a propagation of concentration front. We call this chemical waves ;
• and the other one has a stationary character. We can observe some structures with periodic concentrations in space : the Turing structures.

Chemical waves
The discovery of chemical waves was due to A. Zhabotinsky [33]. The first systematic works about the BZ reaction were published by A. Winfree en 1972. The experiment below, permits to show the propagation of chemical waves during the BZ reaction, in a thin rest coat. The experiment is quite the same as this one proposed by J. -C. Micheau in [14]. Prepare three solutions at around 20 °C :

• A solution : 5 g de NaBrO₃, 67 mL of distilled water, 1 mL of concentrated sulfuric acid.
• B solution : 5 g de CH₂(COOH)₂, 2,5 g de NaBr, 75 mL of distilled water.
• C solution : 0,35 g de FeSO₄, 7 H₂O, 0,75 g of phénantrolin, 50 mL distilled water and two drops of Triton X-100 (a tensio active agent).

The BZ reaction with malonic acid as an initial substrate, has the inconvenient to create a gas : CO₂. Several possibilities were explored to develop gas-free version of the BZ reaction. In one of this reaction malonic acid is replaced by 1,4-cyclohexanedione or 1-3-cyclohexanedione (CHD) as an initial substrate. The system is : CHD/BrO₃^-/Ce⁴⁺/H⁺.

In 1993, Anatol M. Zhabotinsky and his colleagues demonstrated experimentally reflection and refraction of chemical waves using a reaction in a gel. Reaction-diffusion systems are non linear so it's surprising for chemical waves to follow Snell's law. By solving the reaction-diffusion equations, R. Dilao and J. Sainhas of the instituto Superior Técnico Lisboa, Portugal proved mathematically that chemical waves obey Snell's law [40], [6].

The Turing's structures
The english mathematician Alan Turing, tried to establish a theory of morphogenesis. In an item published in 1952, called : The chemical basis of morphogenesis [15], he showed how a chemical reaction coupled with a phenomenon of diffusion, could deal to spatial periodic distributions of the concentrations of some chemical compounds. The observation of the Turing's structure needs some experimental conditions : all the phenomenons of convection must be avoided and then the transportation of compounds must be due to the diffusion only. The reaction is sometimes made in a gel [19]. In 1989, the P de Kepper group tried to visualize I^-, in the CIMA (chlorite, iodide, and malonic acid). In a gel, after the addition of starch (an indicator), these research workers saw some regular rows of task in the reactor as Turing had predicted them. The theoretical calculations in the thermodynamic of irreversible process, show that the phenomenon appears only if the compounds have very different coefficients of diffusion [1]. The starch is a big molecule which diffuse slower than I^- in the gel and this difference permits the observation of the Turing's structure [7].

Some thermodynamics developments

The First Law
The First Law consists in admitting that all the thermodynamical systems have a state function called internal energy U which depends on the parameters of these systems. This energy evoluates if there is exchange between the system and its environment. For a closed system :

dU = dQ + dW

The Second Law
If we pour a drop of ink in a glass of water, an irreversible diffusion appears and in a few minutes, the ink occupies all the volume of water. The Second Law foresees the spontaneous evolution of a transformation. A new function appears. It' S : the entropy. There were several wordings for this Law. The most useful to explain irreversible phenomenons was formulated by I. Prigogine (a Belgian chemist born in Russia). He obtained in 1977 the Nobel prize for his works about thermodynamics. His wording is :

dS = d_iS + d_eS

• d_eS is due to the exchange of heat with the environment. If T_E is the temperature of the environment :

  d_eS = dQ/T_E
  

  if a system doesn't exchange heat :

  d_eS = 0

  Even if it exchanges energy by works. So this principle establishes a difference between Q and W.

• d_iS is due to the internal creation of entropy. The sign of d_iS depends on the situation :

The entropy isn't a conservative function like U.

Reversible transformation
Reversible transformations are ideal and we can describe them by a succession of equilibrium states between the system and its environment during the evolution from the initial state to the final state and we can reverse the sense of time and then recome from the final state to the initial one. In this ideal case :

d_iS = 0

Spontaneous transformation

For these transformations :

d_iS > 0

Chemical affinity
When there is a chemical reaction in a system, the entropy can be considered like a function of the energy U, the volume V and the quantities of material, n_k. In a closed system, the different n_k are linked by the stoichiometry of the reaction. Their variations can be expressed with only one variable : the advancement x.

The Belgian chemist de Donder, introduced a new notion : the affinity A (1922) [1], [16], linked to d_iS by the relation :

d_iS = (A/T).dx

where T is the temperature of the system. The rate of reaction v is :

v = dx/dt

And then :

d_iS/dt = (A/T).v

The production of entropy per units of time appears as a multiplication of 2 terms :

• the rate : v = dx/dt which represents a thermodynamic flow ;

• F = (A/T) which represents the thermodynamic force creating the flow v. It constitues the driving force of the reaction.

We can observe two spontaneous transformation where d_iS > 0 splitted by the chemical equilibrium where d_iS = 0 :

d_iS/dt = S (A_n/T).v_n